Simulating high-accuracy nuclear motion Hamiltonians in discrete variable representation using Walsh–Hadamard QROM with fault-tolerant quantum computers

Ákos Nagy
joint with: Michał Szczepanik and Emil Żak

BEIT Canada

Thursday, November 13, 2025

this presentation can be viewed at akosnagy.com/talks/LG_talk/presentation.html

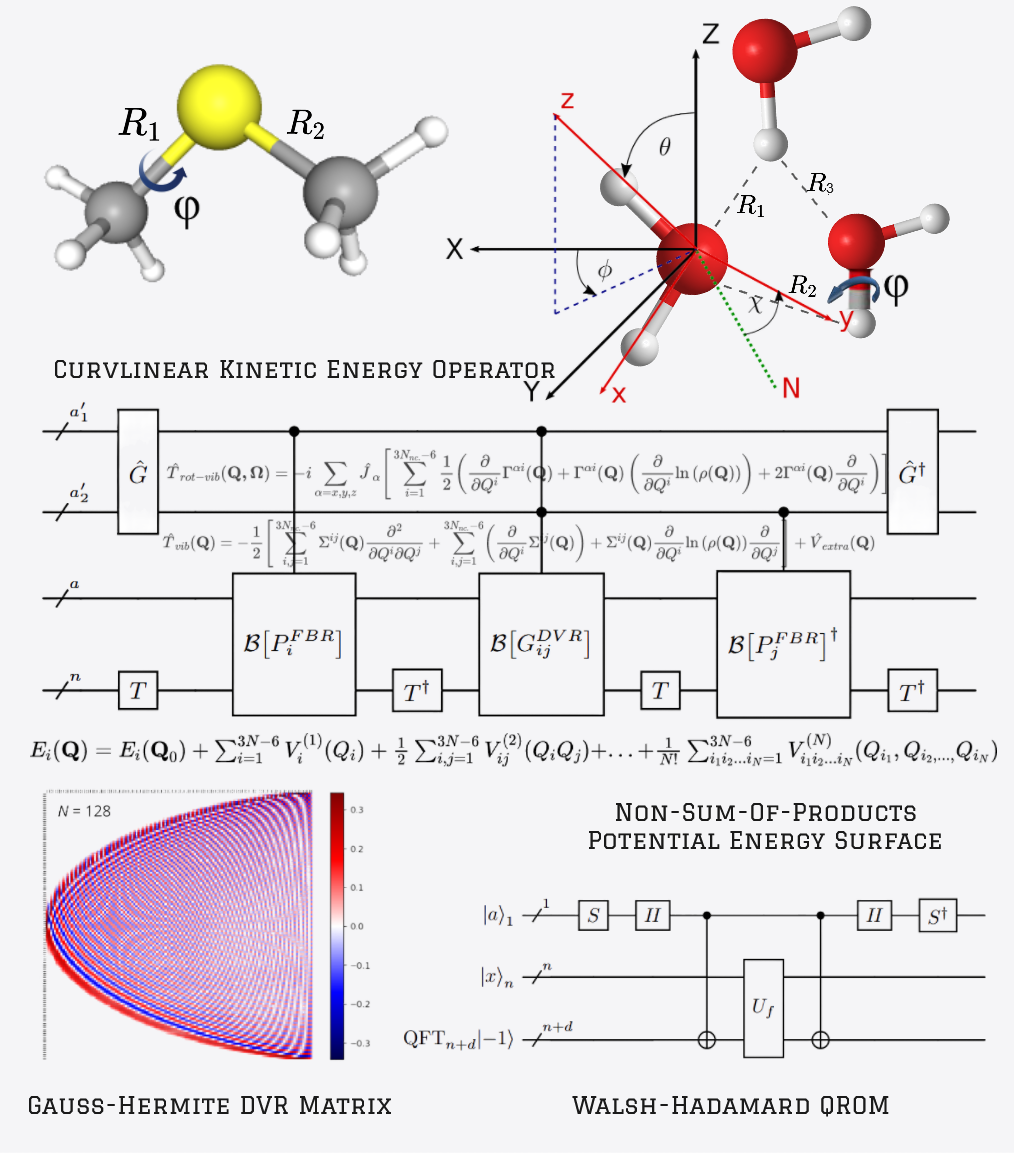
Simulation of nuclear motion Hamiltonians



  • Systems: rovibrational Hamiltonians. A few atoms with rotational and vibrational degrees of freedom.

  • Applications:
    • Spectroscopy
    • Chemical reaction modelling (ultracold physics, biochemistry, catalysis)
    • Astrophysics
    • Atmospheric sciences

  • Problem: the dimension of the Hilbert space grows exponentially with the size of the system. Hence, memory requirements also grow exponentially.

  • Our methods:
    • We use Born–Oppenheimer Hamiltonians with exact kinetic energy part expressed in internal coordinates of the system.
    • Discrete variable representation: Shifts complexities into encoding the Potential Energy Surfaces (PES) at quadrature grid points of the system. Switching to this representation is classically hard, but quantumly cheap!

    • Walsh–Hadamard QROM: Improves the efficiency of the PES encoding, compared to SOTA methods.

  • Example: The quantum volume required for computing the rovibrational spectrum of water can be reduced by a factor of $\approx 10^5$ compared to other quantum algorithms.

QROMs

  • A QROM is a quantum circuit, $U_f$, on $n + d$ qubits, such that \begin{equation} U_f | x \rangle_n | 0 \rangle_d = | x \rangle_n | f(x) \rangle_d, \end{equation} for some $f : \mathbb{F}_2^n \rightarrow \mathbb{F}_2^d$ function.

  • QROMs/QRAMs are used everywhere in quantum computation: Grover Search, Quantum Simulations, Optimization problems, QML...

  • Most common usage for QROMs is diagonal unitary synthesis: \begin{equation} D_\theta | x \rangle_n = e^{i \pi \theta (x)} | x \rangle_n, \end{equation} for some $\theta : \mathbb{F}_2^n \rightarrow [- 1, 1)$. $D_\theta$ can typically be synthesized by one or two calls to some $U_f$.

  • This is also how they show up in our quantum simulations, where they are the most resource-intensive subroutine of the algorithm.

  • We are interested in QROM designs that are efficient in a fault-tolerant setting! This means they are decomposed in a Clifford + Magical gates set.

QROMs (continued)

  • Cliffords: $H$, $S$, $CX$.

  • Magic: Toffoli or $T$. These are more (but not infinitely more) costly, than Cliffords.

  • Resources:
    1. Cost = $C + F \cdot M$, where $1 \ll F \leqslant 300$
    2. Number of ancillas.

  • We constructed QROMs for certain nuclear motion Hamiltonians that outperformed other SOTA implementation in both of those metric.

QROMs (state-of-the-art)

  • The best-known and most commonly used QROM implementation is called the Select–Swap method.

  • This design is sequential in the nonzero values of $f$.

  • Thus, it is useful when the $f$ is sparse.

  • The Select–Swap QROM is, in fact, a family of implementations, parametrized by $1 \leqslant \lambda$. Increasing $\lambda$ decreases the number of Toffolis and the overall circuit depht, but increases the number of ancillas.

  • Resources:
    1. Toffoli count $\approx \tfrac{N_f}{\lambda} + 2 d \lambda$.
    2. Clifford count $\approx d N_f$.
    3. Number of ancillas = $\lambda d$.

  • The Toffoli count is minimized for $\lambda \approx \sqrt{\tfrac{N_f}{2 d}}$.

  • This is Toffoli-optimal, but comes at the cost of $\approx \sqrt{d N_f}$ ancillas. When $N_f = 2^n$ and $n \approx 100$, this comparable to the number of fermions on Earth.

  • No proof for efficiency when Cliffords are accounted for!

Walsh–Hadamard QROM

  • Our method uses the Walsh–Hadamard transform of the input data: \begin{equation} wh(f) (z) := \sum\limits_{x \in \mathbb{F}_2^n} (- 1)^{x \cdot z} f(x). \end{equation}

  • This design is sequential in the nonzero values of $wh(f)$.

  • Thus, it is useful when the $wh(f)$ is sparse!

  • Resources:
    1. Toffoli count $= O \left( d W_f \right)$.
    2. Clifford count $= O \left( d W_f \right)$.
    3. Number of ancillas = $O(d)$.

  • High level idea of the construction:
    1. The parities $(- 1)^{x \cdot z}$ can be computed with $O(1)$ $CX$ gates on the key registers.
    2. Controlled by the parity, a $wh(f)(z)$ adder/subtractor acts on the value register (costs $O(d)$ Toffolis and $CX$ gates).

Walsh–Hadamard QROM (continued)

  • Nontrivial observation: $wh(f)$ is sparse, or sparsely approximatable, if $f$ is smooth enough.

  • Such functions arise, for example, as Potential Energy Surfaces (PES) that need to encoded when simulating nuclear motion Hamiltonians:

Future plans

  • Study further examples from Quantum Simulations.

  • Understand, both qualitatively and quantitatively, where the savings are coming from.
    We suspect that the asymptotic costs can be understood in terms of analytic properties of the function (number of variables, norm of the derivatives, etc.)

  • We expect further cost reductions when the QROM is more carefully integrated into the algorithm.

  • We already have results with Randomized Compilations.

  • Hybridization with existing methods is possible!

Thank you for your attention!