Grover Fixed Point Search for QUBO
Grover's Search Algorithm
- Built to find a marked state in database of unsorted unmarked ones.
- Done through iterative application of reflections.
- Quadratic speed up as $N$ increases.
The Soufflé Problem
- Grover's struggles when the number of target states is unknown (the number of iterations is also unknown).
- With too few rotations, we "undercook" the state.
- Too many rotations and we "overcook" the state.
Solution: Grover Fixed Point Search
- A generalization of Grover's Search Algorithm.
- Yoder–Low–Chuang (2014): Phases are added to the reflection oracles based on success probability.
- As the number of iterations increase, the probability of success can only increase.
- Eliminates the soufflé problem and maintains the quadratic speed up.
Quadratic Unconstrained Binary Optimization (QUBO) problems
- Problem: given a quadratic (real-valued) function, $f$, on $n$ (classical) bits, find its maximum.
- Such a function is given by a symmetric $n$-by-$n$ matrix, $Q$, and a constant $c$. (WLOG: set $c = 0$.)
- MaxCut is QUBO with $Q = $ Graph Laplacian.
Circuit design
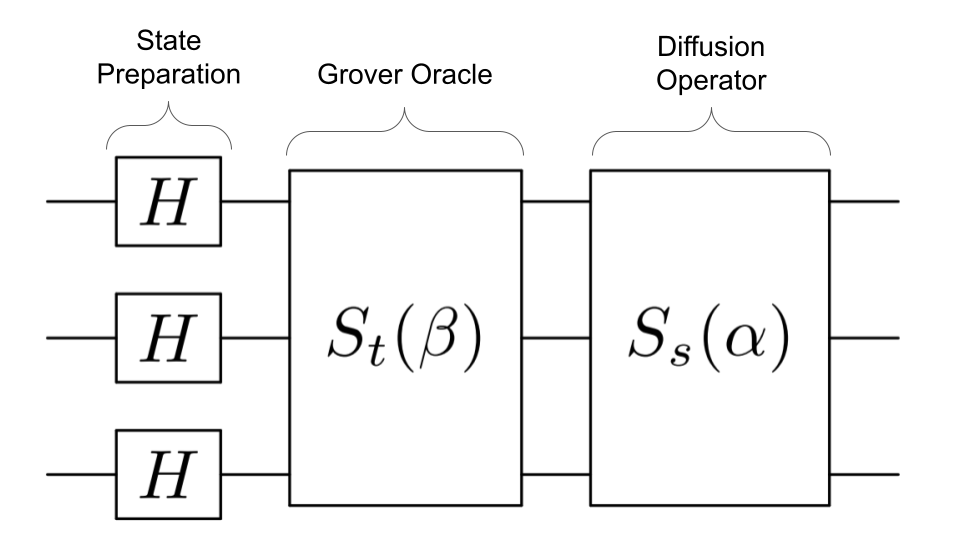
- State Preparation: Equal superposition of solutions and ancillas
- Grover Oracle: Marks desired states with some phase adjusted based on the success probability
- Diffusion Operator: Amplifies marked state
- The last two steps are repeated for all angles $\alpha$ and $\beta$.
Oracle Overview
- Digitize values into ancillas.
- Mark desired states (first ancilla becomes 1 when value is above or on threshold).
- Reset ancillas to threshold value.
- Based on Gilliam–Woerner–Gonciulea (2021): $S_t$ uses $O \left( \ln \left( m \right) \right)$ ancillas.
Example: MaxCut
- For a graph, $G = (V, E)$, find $S \subset V$ so that
\begin{equation}
\mathrm{cut}_G (S) = \left| \left\{ (v, v^\prime) \in E : v \in S \: \& \: v^\prime \notin S \right\} \right|,
\end{equation}
is maximal.

- Recall that MaxCut is QUBO with $Q = $ Graph Laplacian.
More about MaxCut
- MaxCut is NP-hard.
- We only have polynomial time MaxCut-approximations.
- Goemans–Williamson Algorithm: polynomial time algorithm to get a cut at least $\approx 88$% of MaxCut.
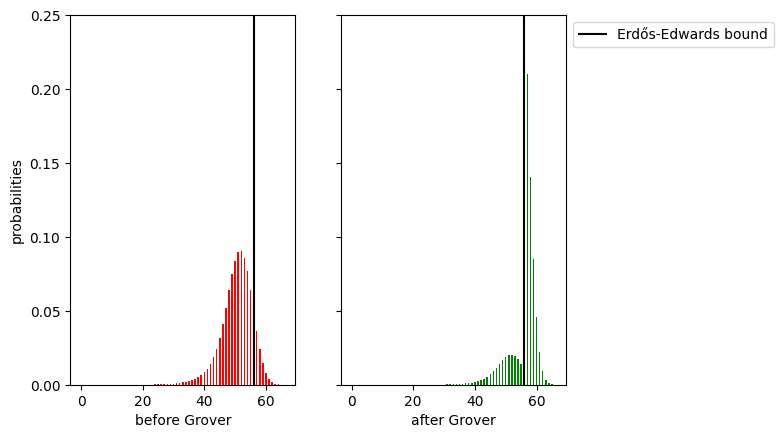
- Erdős–Edwards bound for the maximal cut of connected graphs:
\begin{equation}
\mathrm{MaxCut}_G \geqslant \tfrac{2 m + n - 1}{4}, \quad \left( n = |V|, \: m = |E| \right).
\end{equation}
Can be found in $O \left( n^4 \right)$ time.
Results
- For graphs less than or equal to 20 verticies and with target probability $\geqslant 90$%, $l = 1, 2$ suffices.
- Simulation with the noise model of a modern, all-to-all connected Quantum Computer (IonQ's Harmony) suggests that the noise of either oracles destroys most of the results when $n \geqslant 6$.
- This all works for any QUBO problem with minimal modification.
- In fact, works for all binary optimization problems (short term #1).
- Note: we pre-computed the exact ratios of marked states; in lieu of that, one can also use an adaptive version (short term #2).
Example
Erdős–Rényi-graph with $p = 0.5$, $|V| = 20$, & $|E| = 101$
Simulation without noise
| vertices |
20 |
| edges |
101 |
| $\mathrm{MaxCut}$ |
66 |
| Erdős–Edwards |
56 |
| random chance |
13.98% |
| $\delta$ |
0.93 |
| Query complexity |
1 |
| success probability |
80.89% |
| expectation |
55.87 (+5.37) |
| ancillas |
7 |
| gate count |
8097 |
| circuit depth |
4009 |
| simulation time |
$\sim$ 2 minutes |
cut distributions
Future plans/ideas
- Benchmark against existing algorithms.
- Refine and study the adaptive variant.
- Math problem: given a QUBO instance, can we bound the ratio of good configurations polynomially, from below?
- More sci-fi: This construction can be used as an (approximate) Grover mixer for QAOA.
- The oracle design can be used immediately for Threshold-QAOA (cf. Golden–Bärtschi–O’Malley–Eidenbenz, 2021).
Thank you for your attention!




